The following post is based on a presentation that I gave early last month (August 2009). The occasion was a symposium of NSF REU summer programs in the San Francisco Bay area. The California Academy of Sciences hosts the oldest such program in the region, the Summer Systematics Institute. I was asked to give the keynote presentation. I thought for sometime about what would be an appropriate topic for an audience of my peers and very bright and industrious young college students. I decided to chat about networks (of course), the opportunities available to scientists as humans in the modern world, and the responsibility of scientists toward that world. I'd like to share this essay with my readers, and will do so over the next few posts. So here it is...
Let's begin with a riddle. What do Kevin Bacon, Adolf Hitler, ecosystems and science education have in common? If we count persons that I know personally, then I am only 3 steps, or links, removed from both Hitler and Mr. Bacon. Now, for those of you who may know me, and are disturbed by your newly discovered connection to Hitler, or maybe Mr. Bacon, don't worry; I am only 4 steps removed from Mahatma Gandhi. I find these facts to be remarkable given that I grew up in a world of 6 billion humans. Doubtless, many of you have heard of the 6 degrees of Kevin Bacon game, where so many Hollywood actors, and by extension you and I, are on average only 6 steps removed from Mr. Bacon. This is, again on average, true of the global human population. Even as the global population grows toward 10 billion, we are learning that we live in a small world, and that the world is in fact becoming smaller for many of us.
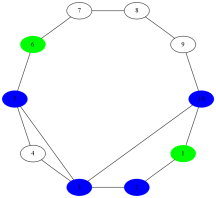
This idea can be illustrated very nicely with graph theory and network visualizations. Imagine a network, or neighbourhood, where each person knows only their immediate neighbours. In order to get to know the person furthest removed from you, you have to become acquainted with (N-2)/2 other people (where N is the total number of people). This distance grows with the size of the population. If we assume, however, that there is some small chance that you know someone at some distance, a very social neighbour for example, and we add that connection, Voila! The number of steps now falls dramatically. A family acquaintance who writes Indian literature is my link to the Mahatma. Note that these results cannot be obtained by simply randomizing the network; on average, those paths would still be pretty long. What we can do, by adding a few links strategically, or by creating a person who is a real social hub, is to create a small world. That's why I am so close to Mr. Bacon. His friends call him Kevin.
(The first image is from the BBC's "Six Degrees of Separation")